Vom Erstbeweger zur Unvollständigkeit – oder: Warum nicht alles beweisbar ist

Haben Sie sich jemals gefragt, wer oder was der Ursprung von allem ist? Diese scheinbar einfache Frage führt uns zu einem spannenden philosophischen Problem: dem infiniten Regress.

Infinit regress – Wer hat Gott erschaffen?

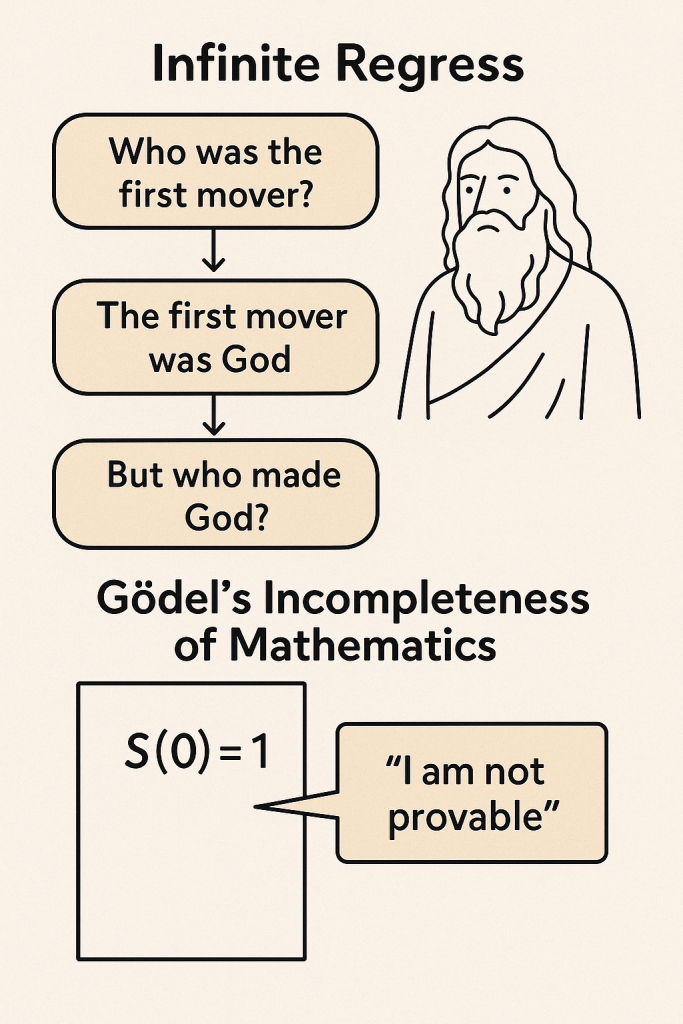
Stellen Sie sich vor, alles hätte eine Ursache. Ein Stein bewegt sich, weil er gestoßen wurde. Doch wer oder was hat die erste Bewegung ausgelöst – wer war der Erstbeweger? Manche sagen, dieser Erstbeweger sei Gott. Doch dann kommt unweigerlich die Frage auf: Wer hat Gott erschaffen? Sobald man versucht, eine Ursache für die Ursache zu finden, gerät man schnell in eine endlose Kette von Fragen, ohne jemals eine endgültige Antwort zu erreichen. Genau das nennt man einen infiniten Regress.

Gödel und die Grenzen der Mathematik

Nun könnte man meinen, dass solche Probleme nur in Philosophie oder Religion auftreten. Überraschenderweise zeigt sich jedoch ein ähnliches Problem sogar in der Mathematik – einer Disziplin, die wir gern für absolut eindeutig und widerspruchsfrei halten. Der österreichische Mathematiker Kurt Gödel hat genau dies 1931 bewiesen.

Gödel fand heraus, dass in jedem ausreichend komplexen logischen System, wie etwa der Mathematik, wahre Aussagen existieren, die nicht bewiesen werden können. Anders gesagt: Selbst die Mathematik kann nicht alles beweisen, was wahr ist. Dies nennt man “Gödels Unvollständigkeitssatz”.

Warum passiert das?

Die Erklärung liegt in einer besonderen Art der Selbstreferenz, ähnlich wie das Problem des infiniten Regresses. Gödel hat gezeigt, dass mathematische Systeme Aussagen enthalten können, die über sich selbst sprechen – vergleichbar mit der Aussage: “Ich bin nicht beweisbar.” Versucht man, diese Aussage zu beweisen, entsteht ein Widerspruch. Versucht man hingegen, sie nicht zu beweisen, bleibt sie wahr, aber eben unbeweisbar. Genau diese paradoxe Situation verdeutlicht die Grenze dessen, was Mathematik leisten kann.

Die philosophische Dimension

Genau wie die philosophische Frage nach dem Erstbeweger uns zeigt, dass nicht alles erklärbar ist, zeigt uns Gödel, dass auch in der Mathematik nicht alles beweisbar ist. Beide Konzepte weisen darauf hin, dass unser Streben nach ultimativer Erklärung oder Begründung Grenzen hat – Grenzen, die tief in der Struktur unseres Denkens verankert sind.

Fazit

Ob Philosophie, Religion oder Mathematik – irgendwann stoßen wir stets auf fundamentale Grenzen. Dies ist keine Schwäche, sondern vielmehr eine Aufforderung zur Demut gegenüber der Komplexität und Schönheit der Welt, die wir wahrscheinlich niemals vollständig erfassen werden.