Dieser Blog basiert auf dem Buch Können wir die Welt verstehen? von Josef M. Gassner und Jörn Müller, insbesondere auf Kapitel 5. Das Buch wird von einer gleichnamigen YouTube-Reihe begleitet, die ich Physikinteressierten wärmstens empfehlen kann: von Aristoteles zur Stringtheorie. Neben der Physik wird in faszinierender Weise die Geschichte des menschlichen Erkenntnisgewinns über die Natur und ihre Ursprünge dargestellt. Auch ihr Folgeband “Kosmologie. Die größte Geschichte aller Zeiten” ist an Dramatik kaum zu überbieten.
Zu Beginn des 20. Jahrhunderts veränderten zwei neue Strömungen in der Physik das Weltbild der Menschheit grundlegend. Einerseits ebnete Max Planck mit seiner theoretischen Erklärung der Strahlungsdichte eines schwarzen Körpers im Jahr 1900 den Weg für einen neuen Zweig der Physik: die Quantenmechanik. 1918 erhält Planck dann für seine theoretische Erklärung der Strahlungsdichte eines schwarzen Körpers den Nobelpreis. Andererseits formulierte Albert Einstein 1905 die Spezielle Relativitätstheorie (SRT) und 1915 die Allgemeine Relativitätstheorie (ART). Interessanterweise erhielt Einstein jedoch nie den Nobelpreis für seine Relativitätstheorien, sondern stattdessen 1921 für den fotoelektrischen Effekt – ein Werk, das ironischerweise die Grundlage für die Solarindustrie legte und zugleich die Quantenmechanik nachhaltig beeinflusste.
Beide Zweige der Physik führen letztlich zu einem Bruch mit der anschaulichen Vorstellungskraft und dem sogenannten ‚gesunden Menschenverstand‘. In diesem Blog wird die SRT näher betrachtet, denn für ihr Verständnis benötigt man – man mag es kaum glauben – als mathematisches Werkzeug lediglich den guten alten Pythagoras. Zudem lässt sich aus der SRT die wohl berühmteste physikalische Formel überhaupt ableiten: E=mc².
In einem folgenden Blog werde ich auf die Allgemeine Relativitätstheorie (ART) eingehen, dabei jedoch versuchen, die deutlich komplexere Mathematik – insbesondere die Verwendung von Tensoren (mehrdimensionale Operatoren, die partielle Differenzialgleichungen für Energie und Impuls enthalten) – so weit wie möglich außen vorzulassen. Für das Verständnis der ART reicht die Kenntnis des Pythagoras leider nicht mehr aus.
Anschließend folgt eine längere Blogserie zum Thema Quantenmechanik. Wir beginnen mit Plancks Strahlungsdichtegesetz für den schwarzen Körper und seiner Quantisierung der Energie eines harmonischen Oszillators, gefolgt von Einsteins Fotoelektrischem Effekt und dem Doppelspalt-Experiment mit seinen faszinierenden Interpretationen. Und genau in dieser Reihenfolge verabschieden wir uns mit zunehmender Beschleunigung vom ‚gesunden Menschenverstand‘.
Lassen wir uns also auf die physikalische Sicht der Relativität ein. Einstein war ein begeisterter Zugreisender, insbesondere auf den Strecken zwischen Deutschland und der Schweiz. Die Eisenbahn, das technische Wunderwerk seiner Zeit, ermöglichte es vielen Menschen, lange Distanzen in vergleichsweise kurzer Zeit zu überwinden. Kein Wunder also, dass viele seiner berühmten Gedankenexperimente das Zugfahren zum Thema haben.
Ob Einstein mit der heutigen Deutschen Bahn die Relativitätstheorie hätte entwickeln können, bleibt eine offene Frage.
Starten wir also unser Gedankenexperiment:
Es ist Abend, und ich sitze in einem klassischen Zugabteil (kein Großraumabteil), das noch im Bahnhof steht. Ich habe gerade mein Gepäck verstaut und hoffe, dass ich nichts vergessen habe. Glücklicherweise habe ich einen Fensterplatz. Am Nachbargleis steht ebenfalls ein Zug, der auf seine Abfahrt wartet. Während ich mich kurz mit einem Mitreisenden unterhalte, überkommt mich für einen Moment ein seltsames Gefühl.
Sind wir schon losgefahren? Aber das kann nicht sein – das Gefühl der Beschleunigung fehlt. Ich schaue aus dem Fenster und sehe, wie sich die Fenster der beleuchteten Abteile des anderen Zuges aneinander vorbeischieben. Etwas bewegt sich definitiv, aber bin ich es? Mein Zug? Erst ein Blick in die entgegengesetzte Richtung, durch die Tür des Abteils, zeigt mir, dass mein Zug noch immer am Bahnsteig steht und sich nicht vom Fleck bewegt hat. Was ist passiert? Etwas hat sich doch bewegt!
Die Erklärung für dieses Phänomen ist einfach: Das Gehirn kann beim Anblick der sich verschiebenden Zugfenster aufgrund der Bewegung eines Zuges nicht sofort erkennen, welcher Zug sich tatsächlich bewegt. Erst die Erfahrung, dass eine Zugfahrt ohne das leichte Rucken der Beschleunigung nicht begonnen haben kann, weckt Zweifel daran, ob man wirklich losgefahren ist. Deshalb sucht man instinktiv nach einer Bestätigung und schaut auf die andere Seite des Abteils, wo sich die Situation klärt. Die Verwirrung des Gehirns ist also berechtigt – aus einer anderen Perspektive betrachtet, liegt es sogar richtig.
Nun stellen wir uns einen Reisenden im Zug vor, der gerade den Bahnhof verlässt. Er sitzt ebenfalls am Fenster und beobachtet, wie sich der Nachbarzug samt Bahnhof von ihm entfernt. Selbstbewusst legt dieser Reisende ein Koordinatensystem mit dem Ursprung in der Mitte seines Körpers an und stellt fest: Er ruht im Ursprung, während sich der Nachbarzug und der Bahnhof von ihm wegbewegen.
In der folgenden Animation wird der Aspekt der Relativität anschaulich dargestellt. Im ersten Beispiel wird eine Orange von einer Lokomotive, die über eine hohe Eisenbahnbrücke fährt, herabgeworfen. Auf der linken Seite beobachtet jemand von der Lok aus den Wurf und sieht, wie die Orange immer schneller geradewegs in die Tiefe fällt. Genau das würde auch jemand beobachten, der auf der Brücke steht und eine Orange hinunterwirft.
Ganz anders sieht der Wurfverlauf für einen Beobachter aus, der unten steht und die Szene betrachtet. Aus seiner Perspektive beschreibt die Orange eine Wurfparabel. Wie kommt diese zustande? Die Lokomotive und die Orange besitzen einen Impuls m*vZug in Fahrtrichtung des Zuges. Da der Impuls – ähnlich wie die Energie – eine Erhaltungsgröße ist, behält die Orange diesen Impuls auch nach dem Fall bei. Durch das Fallenlassen der Orange geht dieser Impuls nicht verloren. Daher nimmt der ruhende Beobachter eine Überlagerung der horizontalen Bewegung des Zuges und der durch die Gravitation nach unten fallenden Orange wahr.
Der zweite Teil der Animation zeigt eine abstrahierte Darstellung: die ruhende Orange im Zug mit einem Koordinatensystem, dessen Ursprung sich im Mittelpunkt der Orange befindet. Aus dieser Perspektive befindet sich die Orange relativ zu sich selbst in Ruhe. Anders sieht es ein stationärer Beobachter, der durch eine gläserne Front die Orange auf dem Boden des Zuges liegen sieht.
Im dritten Teil der Animation rollt die Orange über den Boden des Zuges. Ein Zuggast nimmt die Orange als rollend, mit einer Geschwindigkeit vOrange wahr. Der stationäre Beobachter von außen hingegen sieht eine Orange, die sich mit der deutlich höheren Geschwindigkeit vOrange + vZug bewegt.
Wie oben angedeutet, verwendet der Physiker unterschiedliche Koordinatensysteme, um die verschiedene Wahrnehmung desselben Vorgangs aus unterschiedlichen Perspektiven zu beschreiben. In den obigen Beispielen wird immer vorausgesetzt, dass es einen ruhenden, stationären Beobachter gibt und relativ zu diesem ein System, das sich mit konstanter Geschwindigkeit, also ohne Beschleunigung, entfernt. Dies ist ein Spezialfall und bildet die Grundlage für die Spezielle Relativitätstheorie.
Kein Geringerer als Galileo Galilei widmete sich diesem Problem und führte das Konzept der sogenannten Galileischen Transformation ein. Dabei beschrieb er ein ruhendes Koordinatensystem mit den kartesischen Koordinaten x, y und z und ein Koordinatensystem, das sich mit konstanter Geschwindigkeit bewegt, mit den Koordinaten x’, y’, z’. Da der gesunde Menschenverstand nahelegt, dass die Zeit absolut ist und nicht vom Koordinatensystem abhängt, gilt für die Zeit t = t’.
Um dies verständlich zu machen, stellen wir uns vor, wir haben zwei Beobachter: einen, der in einem ruhenden Zug sitzt, und einen anderen, der in einem Zug sitzt, der sich mit konstanter Geschwindigkeit bewegt. Der ruhende Beobachter misst die Position eines Objekts im Raum mit den Koordinaten x, y, z. Der Beobachter im bewegenden Zug misst die Position desselben Objekts, aber in seinem eigenen Koordinatensystem, das wir mit x’, y’, z’ bezeichnen.
Die Galileische Transformation beschreibt, wie die Koordinaten in den beiden Systemen zusammenhängen. Wenn wir uns auf eine Bewegung entlang der x-Achse konzentrieren, ist die Transformation ganz einfach:
x’ = x – v * t
Hierbei ist v die konstante Geschwindigkeit, mit der sich der bewegte Zug (das zweite Koordinatensystem) relativ zum ruhenden Zug (dem ersten Koordinatensystem) bewegt. Da die beiden Züge zur gleichen Zeit beobachten, gilt t = t’.
Das bedeutet: Die Position eines Objekts im bewegten System (x’) ist einfach die Position des Objekts im ruhenden System (x) minus dem zurückgelegten Weg des Zuges (v * t). Für die anderen Koordinaten y und z gibt es keine Veränderung, da sie nicht in Bewegungsrichtung liegen: y’ = y und z’ = z.
Diese einfache, intuitive Vorstellung, dass Zeit für beide Beobachter gleich abläuft und dass wir nur die Positionen entlang der Bewegungsrichtung anpassen müssen, bildet die Grundlage für die klassischen, vor-einsteinischen Vorstellungen von Raum und Zeit.
Gegen Ende des 19. Jahrhunderts wurde jedoch immer klarer, dass die Lichtgeschwindigkeit eine besondere Rolle spielt: Sie schien unabhängig von der Bewegung der Erde relativ zur Sonne immer konstant zu bleiben. Dies stellte die klassische Physik vor ein großes Rätsel, da man glaubte, dass Licht wie eine Welle nur durch ein Medium – den sogenannten Äther – übertragen werden könne. Man erwartete, dass die Lichtgeschwindigkeit relativ zur Bewegung der Erde durch den Äther variieren müsste, ähnlich wie die Geschwindigkeit eines Bootes relativ zum Wasserstrom.
Das berühmte Michelson-Morley-Experiment von 1887 versuchte, diese Veränderung der Lichtgeschwindigkeit zu messen, indem es die Lichtgeschwindigkeit in verschiedene Richtungen auf der Erdoberfläche verglich. Doch zu ihrer Überraschung stellten Michelson und Morley fest, dass die Lichtgeschwindigkeit in allen Richtungen gleich war, unabhängig von der Bewegung der Erde durch den angeblichen Äther. Diese unerwartete Konstanz der Lichtgeschwindigkeit führte zu einem fundamentalen Umdenken in der Physik.
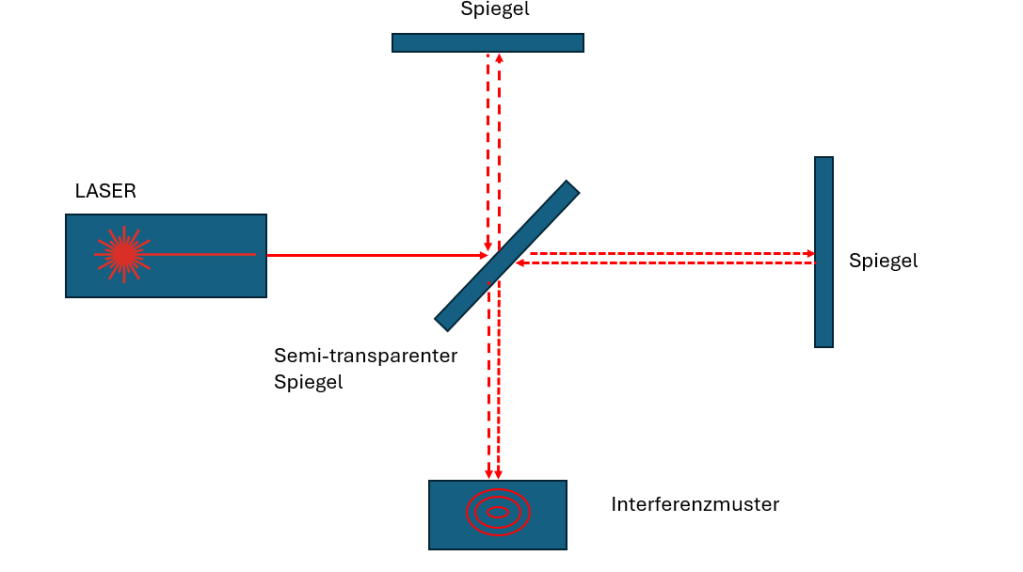
Das Ergebnis des Michelson-Morley-Experiments war einer der entscheidenden Bausteine für die Entwicklung der Speziellen Relativitätstheorie, da es deutlich machte, dass die Lichtgeschwindigkeit eine universelle Konstante ist, die für alle Beobachter gilt – unabhängig davon, wie sie sich bewegen. Diese Erkenntnis zwang die Physiker, die klassischen Vorstellungen von Raum und Zeit radikal zu überdenken.
Die Konstanz der Lichtgeschwindigkeit in allen Bezugssystemen stellt ein Problem für die Galileische Transformation dar, weil sie den grundlegenden Annahmen widerspricht, auf denen die Galileische Transformation beruht.
Um das anschaulich zu erklären, stellen wir uns zunächst einmal die Grundidee der Galileischen Transformation vor: Diese Transformation geht davon aus, dass die Zeit in allen Bezugssystemen absolut ist, das heißt, sie läuft für alle Beobachter gleich ab. Wenn wir uns also in einem fahrenden Zug befinden und ein Objekt im Zug werfen, würde die Geschwindigkeit des Objekts in Bezug auf einen außenstehenden, ruhenden Beobachter einfach die Geschwindigkeit des Objekts relativ zum Zug plus die Geschwindigkeit des Zuges selbst sein. Das ist intuitiv und entspricht unserem Alltagsverständnis.
Jetzt kommt aber das Licht ins Spiel. Nehmen wir an, dass im Zug eine Taschenlampe eingeschaltet wird und ein Lichtstrahl nach vorn ausgesendet wird. Laut der klassischen Physik (und damit auch der Galileischen Transformation) müsste die Geschwindigkeit dieses Lichtstrahls aus Sicht eines außenstehenden Beobachters ebenfalls die Geschwindigkeit des Lichtstrahls relativ zum Zug plus die Geschwindigkeit des Zuges selbst sein – genau wie bei dem geworfenen Objekt.
Das Problem tritt jedoch auf, weil Experimente gezeigt haben, dass das Licht sich für alle Beobachter immer mit derselben Geschwindigkeit bewegt – unabhängig davon, wie schnell sich der Zug oder das Licht relativ zum Zug bewegt. Das bedeutet, ob der Zug fährt oder nicht, jeder Beobachter misst für das Licht immer dieselbe Geschwindigkeit, nämlich etwa 300.000 Kilometer pro Sekunde.
Stellen wir uns vor, dass ein Außenstehender die Geschwindigkeit des Lichtes im Vergleich zum Zug messen möchte. Nach der Galileischen Transformation müsste er eigentlich feststellen, dass das Licht, das vom Zug ausgestrahlt wird, schneller oder langsamer ist, je nachdem, ob der Zug auf ihn zu- oder von ihm wegfährt. Doch das passiert nicht. Die Messungen zeigen, dass die Lichtgeschwindigkeit unabhängig von der Bewegung des Zuges konstant bleibt.
Das bedeutet, die Annahme der Galileischen Transformation – dass sich Geschwindigkeiten einfach addieren – funktioniert für Licht nicht. Denn wenn die Lichtgeschwindigkeit konstant bleibt, kann die Geschwindigkeit des Zuges nicht einfach auf die Lichtgeschwindigkeit „draufgepackt“ werden. Diese Diskrepanz bedeutet, dass das klassische Konzept von Raum und Zeit, wie es durch die Galileische Transformation beschrieben wird, nicht ausreicht, um die Realität zu erklären.
Um dieses Problem zu lösen, musste Albert Einstein eine völlig neue Art des Denkens einführen: die Spezielle Relativitätstheorie. In dieser Theorie wird die Konstanz der Lichtgeschwindigkeit als fundamentales Prinzip anerkannt, und daraus folgt, dass Raum und Zeit nicht absolut sind, sondern relativ – sie verändern sich je nach dem Bewegungszustand des Beobachters. Dies führte zu der revolutionären Erkenntnis, dass Zeit und Raum miteinander verknüpft sind und dass Zeit für verschiedene Beobachter unterschiedlich verlaufen kann, abhängig von ihrer relativen Geschwindigkeit.
Kurz gesagt: Die Konstanz der Lichtgeschwindigkeit widerspricht der Vorstellung, dass man Geschwindigkeiten einfach addieren kann, wie es in der Galileischen Transformation vorgesehen ist, und zeigt, dass unsere herkömmlichen Vorstellungen von Raum und Zeit überdacht werden müssen.
Schauen wir uns das aber noch einmal auf der Formel Ebene an.
Um zu demonstrieren, dass die Galileische Transformation nur gerettet werden kann, wenn man annimmt, dass t ≠ t’ (also die Zeit in den beiden Bezugssystemen unterschiedlich ist), gehen wir durch ein Gedankenexperiment, das die Probleme mit der Annahme von t = t’ verdeutlicht.
Ausgangssituation
Nehmen wir an, wir haben zwei Beobachter:
- Beobachter A ist in einem ruhenden Bezugssystem (z.B. steht auf dem Bahnsteig).
- Beobachter B ist in einem bewegten Bezugssystem (z.B. sitzt in einem Zug, der mit konstanter Geschwindigkeit v nach rechts fährt).
Jetzt senden wir einen Lichtstrahl von der Spitze des Zuges in Fahrtrichtung (nach rechts). Laut der klassischen Physik, die die Galileische Transformation nutzt, sollte die Geschwindigkeit des Lichts aus Sicht von Beobachter A die Geschwindigkeit des Lichts c plus die Geschwindigkeit des Zuges v sein. Aus Sicht von Beobachter B, der sich mit dem Zug bewegt, sollte das Licht einfach die Geschwindigkeit c haben, weil es relativ zu ihm ausgesendet wird.
Galileische Transformation mit t = t’
Die Galileische Transformation geht davon aus, dass die Zeit für beide Beobachter gleich ist, also t=t′. Dies führt zu folgender Formel für die Position x′ des Lichtstrahls relativ zu Beobachter B im Zug:
x′=x−vt
Nehmen wir an, das Licht bewegt sich im ruhenden System (aus Sicht von Beobachter A) mit einer Geschwindigkeit c fort. Dann wäre: x=ct
Einsetzen in die Galileische Transformation:
x′=ct−vt
x′=t(c−v)
Diese Formel bedeutet, dass das Licht für Beobachter B mit einer geringeren Geschwindigkeit c−v erscheint, was dem Prinzip widerspricht, dass die Lichtgeschwindigkeit in allen Bezugssystemen gleich c sein sollte. Hier zeigt sich das Problem der Annahme t=t′
Anpassung der Transformation: t ≠ t’
Um die Konstanz der Lichtgeschwindigkeit zu retten, müssen wir annehmen, dass die Zeit in den beiden Bezugssystemen unterschiedlich verläuft. Dies führt zu der Idee, dass die Zeit für Beobachter B langsamer oder schneller verlaufen muss, je nachdem, wie er sich relativ zu Beobachter A bewegt. Das bedeutet, dass t und t′ nicht gleich sein dürfen.
Wir müssen also die Zeit in das Transformationsgesetz einbeziehen. Statt einfach t=t′ anzunehmen, postulieren wir, dass t und t′ durch eine Funktion miteinander verbunden sind, die von der Relativgeschwindigkeit abhängt.
Diese Funktion wird in der Physik Gammafaktor bzw. Lorentzfaktor genannt, nach dem niederländischen Mathematiker Hendrik Antoon Lorentz, der als erste diese Beziehung aufstellte, aber die physikalische Interpretation doch lieber Einstein überließ, zu gewagt schien sie ihm.
Und jetzt kommt endlich die Stunde des Pythagoras.
Um den Lorentzfaktor herzuleiten, verwenden wir ein Gedankenexperiment mit einer sogenannten „Lichtuhr“ und den Satz des Pythagoras. Dieses Experiment hilft uns, die Auswirkungen der speziellen Relativitätstheorie und die Rolle des Lorentzfaktors verständlich zu machen.
Was ist eine Lichtuhr?
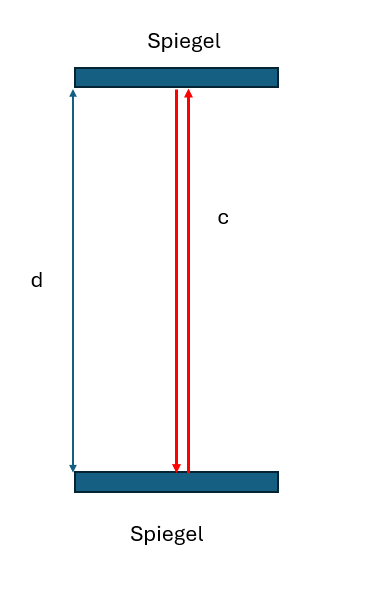
Stell dir eine Lichtuhr als einfaches Gerät vor, das aus zwei parallelen Spiegeln besteht, die sich in einem bestimmten Abstand voneinander befinden. Ein Lichtstrahl wird zwischen diesen beiden Spiegeln hin- und her reflektiert. Jedes Mal, wenn der Lichtstrahl den oberen Spiegel erreicht und wieder zurückgeworfen wird, vergeht eine bestimmte Zeitspanne – nennen wir sie „Tick“.
Die Lichtuhr in einem bewegten Bezugssystem
Zunächst betrachten wir die Lichtuhr in einem bewegten Bezugssystem. Ein Zugfahrer hat die Uhr mit in den Zug genommen. Aus Sicht eines Beobachters, der sich relativ zur Lichtuhr nicht bewegt, aber selbst mit dem Zug fährt, bewegt sich der Lichtstrahl mit der Lichtgeschwindigkeit c senkrecht zwischen den Spiegeln hin und her.
Wenn der Abstand zwischen den Spiegeln d beträgt, dann ist die Zeit, die das Licht benötigt, um von einem Spiegel zum anderen zu gelangen:
t’=d/c
Hier ist t’ die Zeit, die in einem bewegtem System für einen „Tick“ der Uhr gemessen wird.
Die Lichtuhr aus Sicht eines ruhenden Bezugssystems
Jetzt stellen wir uns vor, dass die Lichtuhr mit einer konstanten Geschwindigkeit v relativ zu einem Beobachter in horizontaler Richtung (z.B. nach rechts) bewegt wird.
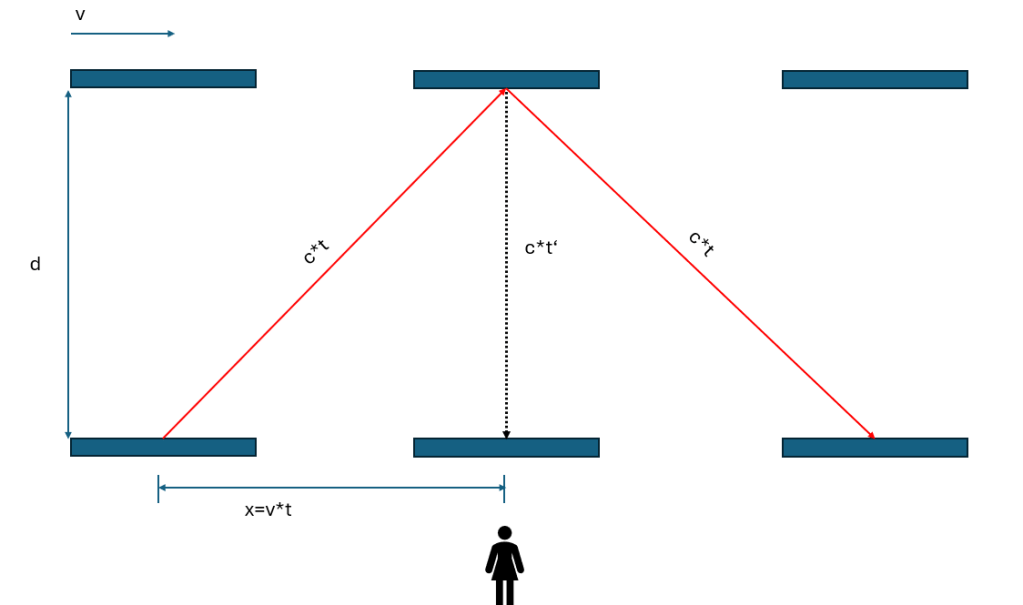
Aus Sicht dieses ruhenden Beobachters macht der Lichtstrahl nicht nur eine senkrechte Bewegung (zwischen den Spiegeln), sondern auch eine horizontale Bewegung (aufgrund der Bewegung der Lichtuhr). Diese horizontale Bewegung bedeutet, dass das Licht, um den oberen Spiegel zu erreichen, eine längere Strecke zurücklegen muss, die eine diagonale Linie bildet.
Herleitung des Lorentzfaktors mit dem Satz des Pythagoras
Um die Strecke, die das Licht in der bewegten Uhr (aus Sicht der Beobachterin am Bahnsteig) zurücklegt, zu berechnen, können wir den Satz des Pythagoras verwenden.
- Strecke, die das Licht in vertikaler Richtung zurücklegt: Diese Strecke ist gleich dem Abstand zwischen den Spiegeln, also d.
- Strecke, die das Licht in horizontaler Richtung zurücklegt: Während das Licht sich von einem Spiegel zum anderen bewegt, hat sich die Uhr auch um eine horizontale Strecke v*t bewegt, wobei t die Zeit ist, die für einen „Tick“ in diesem ruhenden System benötigt wird.
- Gesamte Strecke (Hypotenuse): Die gesamte Strecke s, die das Licht in der bewegten Uhr zurücklegt, bildet die Hypotenuse eines rechtwinkligen Dreiecks, mit d als einer Kathete und v*t als der anderen Kathete. Laut dem Satz des Pythagoras gilt:
s2=d2+(v*t)2
Da das Licht sich immer mit der Geschwindigkeit c bewegt, ist die Strecke s gleich:
s=c*t
Setzen wir das in die Pythagoras-Gleichung ein:
(c*t)2=d2+(v*t)2
Teilen wir die gesamte Gleichung durch c2:
t2=d2/c2+ v2*t2 / c2
Jetzt ziehen wir den Term (v2*t2)/c2 auf die linke Seite:
t2(1−v2/c2)=d2/c2
Nun isolieren wir t:
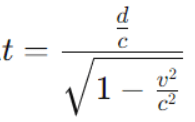
Wir wissen, dass d/c die Zeit t’ ist, die der bewegte Beobachter misst. Damit ergibt sich:
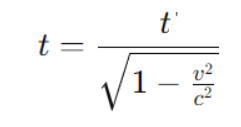
Wobei der Lorentzfaktor γ ist gegeben durch:
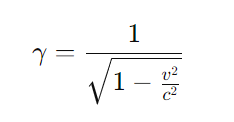
Damit können wir die Zeitdilatation beschreiben: t=γ*t’
Interpretation
- Zeitdilatation: Die Zeit t’, die in einem bewegten System vergeht, ist kürzer als die Zeit t, die in einem ruhenden System vergeht. Das bedeutet, dass eine Uhr, die sich bewegt, langsamer tickt, wenn sie von einem ruhenden Beobachter betrachtet wird.
- Der Lorentzfaktor γ: Der Faktor γ beschreibt, wie stark die Zeit gedehnt wird (=langsamer tickt), je schneller sich das Bezugssystem bewegt. Je näher die Geschwindigkeit v der Lichtgeschwindigkeit c kommt, desto größer wird γ und desto stärker ist die Zeitdilatation.
Ich bin mir sicher, dass die allermeisten trotz des Einsatzes überschaubarer Mathematik (Pythagoras) doch ziemlich skeptisch bleiben. Die Aussage ist, dass bei jemandem, der sich bewegt, die Zeit langsamer abläuft (langsamer tickt) als bei jemandem in Ruhe. Ich bin in meinem Leben oft hektisch hin und her gelaufen, danach fühlte ich mich meistens eher älter als jünger. Und überhaupt, wer hat schon so eine Lichtuhr, typisch Physiker wissen halt nicht eine gute Uhr aus rotierenden Zeigern zu benutzen. Allmählich versteht man, dass Einstein dafür keinen Nobelpreis bekommen hat. Der Hack mit dem Pythagoras ist doch ein Taschenspielertrick?
Nähern wir uns dem Problem der unterschiedlichen Zeiten noch mal von der Physik ohne Mathematik.
Der Unterschied zwischen dem Wurf einer Orange innerhalb eines fahrenden Zuges und dem Einschalten einer Taschenlampe im Zug lässt sich durch die unterschiedlichen Gesetze erklären, die für klassische Objekte (wie die Orange) und Licht (Photonen) gelten.
Wurf einer Orange im fahrenden Zug
Wenn du eine Orange innerhalb eines fahrenden Zuges wirfst, bewegt sich die Orange mit einer Geschwindigkeit, die sich aus zwei Komponenten zusammensetzt:
- Geschwindigkeit des Zuges: Der Zug bewegt sich relativ zum Bahnsteig mit einer bestimmten Geschwindigkeit vZug
- Wurfgeschwindigkeit: Du wirfst die Orange relativ zu dir (und damit relativ zum Zug) mit einer bestimmten Geschwindigkeit vWurf.
Nach den Gesetzen der klassischen Physik, genauer gesagt nach der Galileischen Transformation, addieren sich diese beiden Geschwindigkeiten. Wenn also ein Beobachter auf dem Bahnsteig steht, sieht er die Orange mit einer Gesamtgeschwindigkeit von vGesamt=vZug+vWurf auf sich zukommen.
Der Impuls der Orange, der das Produkt aus ihrer Masse und ihrer Geschwindigkeit ist, wird ebenfalls durch diese Gesamtgeschwindigkeit bestimmt: pOrange = mOrange*(vZug+vWurf)
Licht im Zug
Nun betrachten wir das Einschalten einer Taschenlampe im selben fahrenden Zug. Wenn du die Taschenlampe anmachst, sendet sie Photonen (Lichtteilchen) aus. Nach den Erkenntnissen der modernen Physik, insbesondere der Speziellen Relativitätstheorie, bewegt sich Licht immer mit der gleichen Geschwindigkeit c – unabhängig davon, ob der Zug fährt oder steht.
Wichtige Unterschiede:
- Geschwindigkeit des Lichts: Das entscheidende Merkmal von Licht ist, dass seine Geschwindigkeit c unabhängig von der Geschwindigkeit des Zuges ist. Ob der Zug fährt oder steht, ein außenstehender Beobachter misst immer dieselbe Lichtgeschwindigkeit c. Das bedeutet, dass die Geschwindigkeit des Zuges keinerlei Einfluss auf die Geschwindigkeit des Lichts hat. Im Gegensatz zur Orange addiert sich die Geschwindigkeit des Zuges nicht zur Lichtgeschwindigkeit.
- Impuls des Photons: Ein Photon hat einen Impuls, der durch seine Energie bestimmt ist (nach p=E/c), aber dieser Impuls hängt nicht von der Geschwindigkeit des Zuges ab. Das Licht erhält keinen zusätzlichen Impuls durch die Bewegung des Zuges. Es hat immer denselben Impuls, unabhängig davon, ob es im fahrenden Zug oder im stehenden Zug erzeugt wird.
- Relativität und Universum: Während die Orange sich relativ zum Zug und zum Bahnsteig bewegt und ihre Geschwindigkeit in unterschiedlichen Bezugssystemen anders wahrgenommen wird, ist das Licht „relativ“ zum gesamten Universum unterwegs. Die Lichtgeschwindigkeit ist in jedem Bezugssystem, egal, wie schnell sich das Bezugssystem bewegt, immer gleich. Das ist ein fundamentaler Unterschied, der die klassische Physik (wie bei der Orange) von der Relativitätstheorie unterscheidet.
Klassische Objekte und Licht als Elementarteilchen funktionieren nach unterschiedlichen Regeln und daher machte die Spezielle Relativitätstheorie eine Anpassung der klassischen Konzepte von Raum, Zeit und Bewegung erforderlich.
Aber warum kann man denn davon als normal Sterblicher nichts, aber auch gar nichts merken, schließlich rasen wir doch tagtäglich um “unseren” Globus?
Dazu muss man sich ebendiesen γ Faktor mal ansehen:
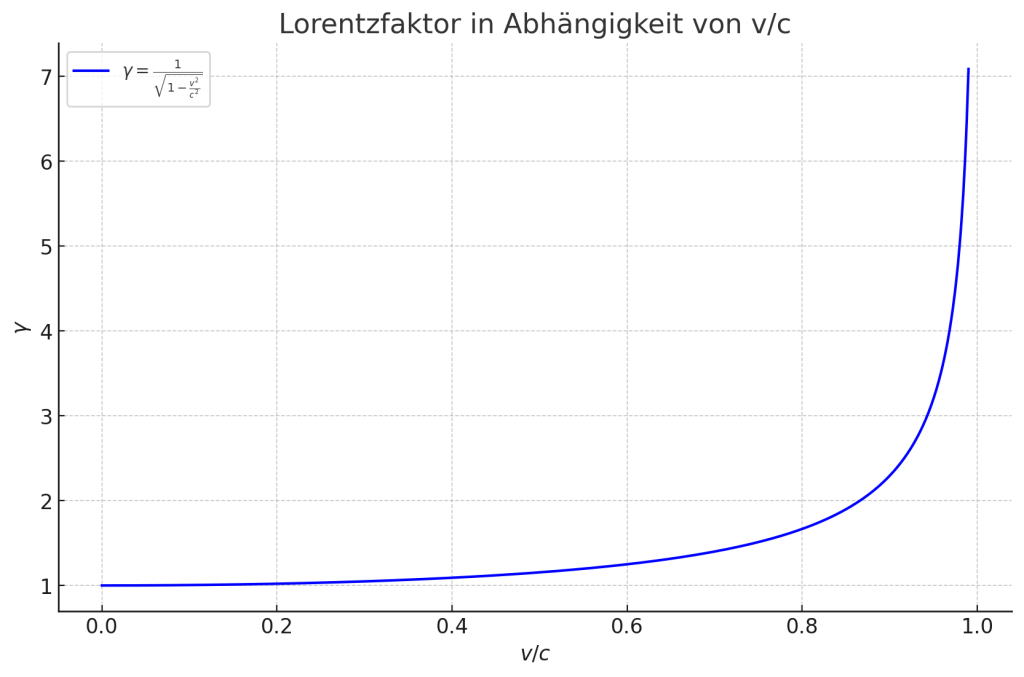
An diesem Diagramm kann man sehen, dass ungefähr ab v>=20 % c der Lichtgeschwindigkeit der γ Faktor etwas von der eins “abhebt“. Schauen wir uns diesen Bereich noch mal genauer an:
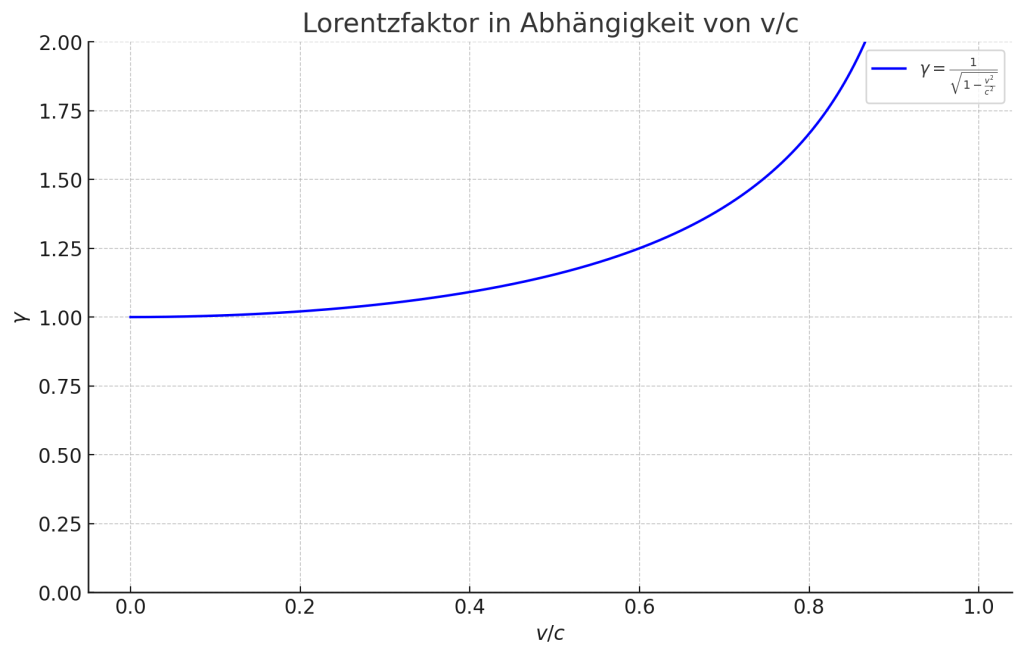
Man sieht auch bei v=20%c ist der γ Faktor weiterhin nicht sehr viel größer als 1. Und da wir normal Sterblichen uns auf diesem Planeten mit weit unter v=20%c bewegen, gilt für uns in ausgezeichneter Näherung γ=1 und damit ist t=t’.
Erst 1971 haben die Astronomen Joseph C. Hafele und der Astronom Richard E. Keating die Spezielle Relativitätstheorie experimentell bestätigt und dazu haben sie auch einigen Aufwand betrieben. Sie bestiegen, mit vier Atomuhren, ein Linienflugzeug und umrundeten damit die Erde je zweimal, zuerst in östlicher, dann in westlicher Richtung. Der Nobelpreis wäre Einstein nun sicher gewesen, aber da war er leider schon 16 Jahre tot und postum wird kein Nobelpreis verliehen.
Hat die Relativitätstheorie denn für uns überhaupt eine Relevanz? Die Antwort ist eindeutig Ja.
In der Allgemeinen Relativitätstheorie, die Einstein 1915 veröffentlichte, begründete er aus der Theorie, also entsprungen aus seinen unnachahmlichen Gedankenexperimenten, dass auch die Gravitation einen Einfluss auf die Zeit hat. In Kurzform ist eine Aussage der ART, dass je weiter man von einem Gravitationszentrum ist, umso schneller die Zeit vergeht. Der Almöhi altert also schneller als die Niederrheiner.
Und es gibt heute ein sehr wesentliches Werkzeug, das ohne SRT und ART nicht wirklich gut funktionieren würde: Das GPS System.
Das GPS-System (Global Positioning System) ist ein beeindruckendes Beispiel dafür, wie die spezielle und Allgemeine Relativitätstheorie in der Praxis angewendet werden, um präzise Ortsmessungen auf der Erde durchzuführen. Obwohl es auf den ersten Blick so aussieht, als ob GPS einfach nur Entfernungen misst, basiert das System tatsächlich auf sehr genauen Zeitmessungen. Welche Rolle spielen die beiden Theorien beim GPS?
Grundprinzip des GPS
Das GPS funktioniert, indem es die Position eines Empfängers (z. B. Ihr Smartphone) auf der Erde berechnet, indem es Signale von mehreren Satelliten empfängt. Jeder Satellit sendet kontinuierlich ein Signal aus, das die genaue Zeit, zu der es gesendet wurde, und die Position des Satelliten zum Zeitpunkt des Sendens enthält.
Ihr GPS-Empfänger nimmt diese Signale auf und berechnet die Zeit, die jedes Signal benötigt hat, um den Empfänger zu erreichen. Da das Signal mit Lichtgeschwindigkeit reist, kann der Empfänger die Entfernung zu jedem Satelliten berechnen, indem er die Zeit mit der Lichtgeschwindigkeit multipliziert. Mit mindestens vier Satelliten kann der Empfänger seine genaue Position auf der Erde bestimmen.
Warum Zeitmessung so wichtig ist
Die Genauigkeit der Ortsbestimmung im GPS hängt von der extrem präzisen Zeitmessung ab. Selbst ein winziger Fehler von einer Milliardstel Sekunde (1 Nanosekunde) in der Zeitmessung kann zu einem Positionsfehler von mehreren Metern führen. Deshalb müssen die Uhren in den GPS-Satelliten extrem genau sein, und hier kommen die relativistischen Effekte ins Spiel.
Relativistische Effekte und das GPS
Es gibt zwei Hauptaspekte der Relativitätstheorie, die das GPS betreffen:
- Spezielle Relativitätstheorie (SRT):
- Die spezielle Relativitätstheorie sagt voraus, dass bewegte Uhren langsamer gehen, verglichen mit Uhren in einem ruhenden Bezugssystem. Die Satelliten bewegen sich mit einer sehr hohen Geschwindigkeit um die Erde (ungefähr 14.000 Kilometer pro Stunde).
- Wegen dieser hohen Geschwindigkeit ticken die Uhren an Bord der Satelliten langsamer als Uhren auf der Erde. Dieser Effekt ist klein, aber messbar: Die Uhren der Satelliten gehen etwa 7 Mikrosekunden (Millionstel Sekunden) pro Tag langsamer als die Uhren auf der Erde.
- Allgemeine Relativitätstheorie (ART):
- Die Allgemeine Relativitätstheorie sagt voraus, dass Uhren in einem stärkeren Gravitationsfeld langsamer gehen. Die Erde erzeugt ein starkes Gravitationsfeld, das auf der Erdoberfläche stärker ist als in der Höhe, in der die GPS-Satelliten kreisen (etwa 20.000 Kilometer über der Erde).
- In der Höhe der Satelliten ist die Schwerkraft schwächer, und daher laufen die Uhren der Satelliten schneller als Uhren auf der Erdoberfläche. Dieser Effekt ist etwas größer als der speziellen Relativitätstheorie: Die Uhren in den Satelliten laufen etwa 45 Mikrosekunden pro Tag schneller.
Korrektur der relativistischen Effekte
Wenn man die Effekte der speziellen und Allgemeinen Relativitätstheorie kombiniert, ergibt sich, dass die Uhren der GPS-Satelliten etwa 38 Mikrosekunden (45 – 7 = 38) pro Tag schneller gehen als Uhren auf der Erdoberfläche.
Dieser Unterschied von 38 Mikrosekunden pro Tag mag klein erscheinen, aber ohne Korrektur würde er zu einem enormen Positionsfehler führen – etwa 10 Kilometer pro Tag! Deshalb wird der Unterschied durch spezielle Korrekturen im GPS-System berücksichtigt:
- Vorstartkalibrierung: Bevor die Satelliten ins All geschickt werden, werden ihre Atomuhren so eingestellt, dass sie auf der Erde etwas langsamer laufen. Sobald sie im Orbit sind und die relativistischen Effekte wirksam werden, laufen die Uhren im Weltraum mit der korrekten Geschwindigkeit, sodass sie mit den Uhren auf der Erde synchron bleiben.
- Kontinuierliche Anpassungen: Die Bodenstationen des GPS-Systems überwachen kontinuierlich die Uhren in den Satelliten und nehmen gegebenenfalls kleinere Anpassungen vor, um sicherzustellen, dass die Zeitmessungen extrem genau bleiben.
Ohne Einstein würde meine Generation wohl noch ihren “geliebten” Falk Plan nutzen.
Aber es gibt noch einen viel tiefer gehenden Grund, warum die Relativitätstheorie uns alles andere als egal sein sollte.
Das Prinzip von Ursache und Wirkung ist eine grundlegende Idee in der Physik: Eine Ursache (z. B. das Schieben eines Balls) führt zu einer Wirkung (z. B. das Rollen des Balls). Dieses Prinzip setzt voraus, dass die Reihenfolge von Ereignissen in allen Bezugssystemen – also für alle Beobachter, unabhängig davon, wie sie sich bewegen – gleich bleibt. Damit dieses Prinzip universell gilt, muss die Lichtgeschwindigkeit in allen Bezugssystemen konstant sein.
Ursache und Wirkung
Das Prinzip von Ursache und Wirkung setzt voraus, dass die Reihenfolge von Ereignissen – also, dass die Ursache immer vor der Wirkung kommt – für alle Beobachter gleich bleibt.
Stellen Sie sich vor, dass die Lichtgeschwindigkeit nicht konstant wäre. Wenn eine Ursache (z. B. das Einschalten einer Lampe) ein Ereignis auslöst (z. B. das Erscheinen eines Lichtstrahls), könnten unterschiedliche Beobachter die Reihenfolge dieser Ereignisse anders wahrnehmen. In einem System, in dem die Lichtgeschwindigkeit nicht konstant ist, könnte es sein, dass ein Beobachter sieht, dass der Lichtstrahl zuerst erscheint und dann die Lampe eingeschaltet wird. Das würde das Prinzip von Ursache und Wirkung verletzen, weil die Wirkung (das Licht) vor der Ursache (dem Einschalten) eintreten würde.
Das Problem ohne konstante Lichtgeschwindigkeit
Wenn die Lichtgeschwindigkeit nicht konstant wäre:
- Unterschiedliche Beobachter könnten widersprüchliche Abfolgen von Ereignissen wahrnehmen. Ein Beobachter könnte sehen, dass A passiert, bevor B passiert, während ein anderer Beobachter sieht, dass B vor A passiert. Das würde die Grundlage unserer physikalischen Gesetze untergraben, die auf einer konsistenten Kausalität basieren.
- Die Kausalität wäre nicht mehr gesichert. Ereignisse könnten in einer Weise wahrgenommen werden, dass Wirkungen vor ihren Ursachen eintreten, was physikalisch unmöglich ist.
Wie die Konstanz der Lichtgeschwindigkeit das Prinzip bewahrt
Die Konstanz der Lichtgeschwindigkeit stellt sicher, dass die Gesetze der Physik, einschließlich des Prinzips von Ursache und Wirkung, für alle Beobachter in allen Bezugssystemen gleich bleiben. Sie zwingt die Natur dazu, Raum und Zeit so zu „verbiegen“, dass die Reihenfolge von Ereignissen konsistent bleibt und Kausalität (also das Prinzip, dass Ursachen immer Wirkungen vorausgehen) für alle gewährleistet ist.
Beenden möchte ich diesen Blog natürlich mit Albert Einstein:
„Das Unbegreiflichste an der Welt ist, dass sie begreiflich ist.“
…und SRT und ART sind essenzielle Bausteine, sie “begreiflich” zu machen.

